Tidymodels and XGBoost; a few learnings
May 27, 2020
R
tidymodels
xgboost
Machine Learning
This post will look at how to fit an XGBoost model using the tidymodels framework rather than using the XGBoost package directly.
Tidymodels is a collection of packages that aims to standardise model creation by providing commands that can be applied across different R packages. For example, once the code is written to fit an XGBoost model a large amount of the same code could be used to fit a C5.0 algorithm.
I will look at a dataset which I have analysed before so I know what to expect and I can compare the tidymodels steps with the ones I implemented originally.
First let’s load the necessary packages. I’ll go through what each of the tidymodels packages does as we go along. We also call doParallel to enable parallelisation.
require(dplyr)
require(rsample)
require(recipes)
require(parsnip)
require(tune)
require(dials)
require(workflows)
require(yardstick)
require(knitr)
require(kableExtra)
require(xgboost)
require(ggplot2)
require(data.table)
#Parallelisation
require(doParallel)
cores <- parallel::detectCores(logical = FALSE)
registerDoParallel(cores = cores)
The first step is to load in the data and apply any relevant pre-processing steps. Here I won’t focus on exploring the data, I’m more interested in following the tidymodels workflow. Also, I can’t talk about the details of this dataset too much for privacy reasons.
This dataset is already split in training and testing.
dim(mwTrainSet)
## [1] 10000 28
Preprocessing
The recipes package can be used to handle preprocessing. You need to build a recipe object that will contain a number of different steps to be followed. This recipe can then be applied to other data, e.g. testing data or new data from the same source.
recipes contains a large number of step functions that aim to account for any necessity you will need in your preprocessing.
myRecipe<- recipes::recipe(outcome ~ ., data=mwTrainSet) %>%
recipes::step_mutate(os = as.factor(os)) %>%
recipes::step_mutate(ob = as.factor(ob)) %>%
step_rm(id) %>%
step_mutate(w50s = ifelse(ds<=0.5,'TRUE','FALSE')) %>%
prep()
This is not my recipe in full but you can see how the process works. os and ob are logical variables and I want to convert them to factors as required by XGBoost. I’m also removing the id variable and creating a new variable w50s.
Here I would like to note that if the logical variables were categorical instead I could have used a step like step_string2factor(all_nominal()) to convert them all into factors at the same time. However, at this time I’m not aware that the required all_logical or step_logic2factor exist so I mutate the variables one by one. There is an open issue with this request here.
You can find a list of all step functions available here.
Now that the recipe is built we can use the bake function to actually run our data through it. I will save the modified dataset in a new object.
proc_mwTrainSet <- myRecipe %>% bake(mwTrainSet)
Cross-validation
Moving along the model-building pipeline we want to create some cross-validation folds from our training set. We will use these folds during the tuning process. For this purpose I use the vfold_cv function from rsample which in my case creates 5 folds of the processed data with each fold split with an 80/20 ratio. I also set the seed for reproducibility.
set.seed(2020)
cvFolds <- mwTrainSet %>%
bake(myRecipe, new_data = .) %>%
rsample::vfold_cv(v = 5)
cvFolds
## # 5-fold cross-validation
## # A tibble: 5 x 2
## splits id
## <named list> <chr>
## 1 <split [8K/2K]> Fold1
## 2 <split [8K/2K]> Fold2
## 3 <split [8K/2K]> Fold3
## 4 <split [8K/2K]> Fold4
## 5 <split [8K/2K]> Fold5
Model specification
We have a processed dataset and we know how we want to validate it so we can now specify the model we want to fit to the data.
xgmodel<-parsnip::boost_tree(
mode = "classification",
trees = 1000, #nrounds
learn_rate = tune(), #eta
sample_size = tune(), #subsample
mtry = tune(), #colsample_bytree
min_n = tune(), #min_child_weight
tree_depth = tune() #max_depth
) %>%
set_engine("xgboost", objective = "multi:softprob",
lambda=0, alpha=1, num_class=3,verbose=1)
xgmodel
## Boosted Tree Model Specification (classification)
##
## Main Arguments:
## mtry = tune()
## trees = 1000
## min_n = tune()
## tree_depth = tune()
## learn_rate = tune()
## sample_size = tune()
##
## Engine-Specific Arguments:
## objective = multi:softprob
## lambda = 0
## alpha = 1
## num_class = 3
## verbose = 1
##
## Computational engine: xgboost
The parsnip package provides an interface for many types of models and the different types of packages that fall into those types. For example, because XGBoost is a boosted tree type of model we use the boost_tree function.
boost_tree provides general parameters that can be used on other boosted tree models. In my specification below I included the XGBoost translation of the boost_tree names.
Many of the parameters have a tune() value assigned to them. This is because later we are going to construct a parameter grid with which we will be able to search what the best parameters are.
Also note that set_engine is where we set that we are using XGBoost and that we can pass XGBoost specific options into this function as well.
By using parsnip you avoid many of the pecularities that XGBoost has. If you used XGBoost directly you would find that you need to encode categorical variables as dummies, you also need to use the specific XGBoost format for matrices xgb.DMatrix and you need to separate out the labels from the predictors.
Here I didn’t need to do any of that because parsnip handles those requirements internally. I think the tidymodels framework makes your life easier but it’s wise to still know how the underlying engines work if you are going to use them.
Tuning the model
We now turn to the dials package. To me this is where tiymodels provides its biggest benefits. It gives the user the ability to tune models in a reproducible manner that is easy to replicate.
First, we need to set up a parameters object with the parameters we want to be tuned.
xgboostParams <- dials::parameters(
min_n(),
tree_depth(),
learn_rate(),
finalize(mtry(),select(proc_mwTrainSet,-outcome)),
sample_size = sample_prop(c(0.4, 0.9))
)
Note that, mtry had to be treated differently and we had to ‘finalize’ it. The reason being that for parameters whose range depends on the data set the user has to provide the range. As mtry() is the number of variables used in the making of each tree we need to bound it by the number of variables available.
mtry()
## # Randomly Selected Predictors (quantitative)
## Range: [1, ?]
finalize(mtry(),select(proc_mwTrainSet,-outcome))
## # Randomly Selected Predictors (quantitative)
## Range: [1, 49]
Another quirk we encounter here is that boost_tree takes the parameter sample_size as integer but XGBoost requires this parameter as a proportion, hence we use sample_prop to specify the range.
Once the parameters to be tuned are defined we can use the grid_max_entropy function to create the grid that will be explored. The max entropy grid is defined like so in the documentation:
Experimental designs for computer experiments are used to construct parameter grids that try to cover the parameter space such that any portion of the space has an observed combination that is not too far from it.
So, we are letting dials define a grid for us that will explore as much as the parameter space as possible. I will set the number of combinations to 100.
set.seed(2020)
xgGrid <- dials::grid_max_entropy(xgboostParams, size = 100)
#knitr::kable(head(xgGrid))
kablify(xgGrid[1:5,])
| min_n | tree_depth | learn_rate | mtry | sample_size |
|---|---|---|---|---|
| 40 | 8 | 0.0017557 | 22 | 0.4202777 |
| 12 | 9 | 0.0000007 | 9 | 0.8233843 |
| 22 | 14 | 0.0000141 | 24 | 0.6387196 |
| 31 | 8 | 0.0000006 | 16 | 0.8828089 |
| 32 | 6 | 0.0001357 | 41 | 0.7991674 |
This is great. When I first fit this model I was using a custom built function for tuning that I found on stackoverflow.
set.seed(1234)
searchGridSubCol <- expand.grid(min_child_weight=c(2),
subsample = c(0.75,0.6,0.9),
colsample_bytree = c(0.6,0.8),
lam = c(2),
alph=c(0),
depth=c(6,10,3),
etaa=c(0.009,0.011,0.013,0.014)
)
ntrees <- 5000
mllHyperparameters <- apply(searchGridSubCol, 1, function(parameterList){
#Extract Parameters to test
currentSubsampleRate <- parameterList[["subsample"]]
currentColsampleRate <- parameterList[["colsample_bytree"]]
currentMCW <- parameterList[["min_child_weight"]]
currentLambda <- parameterList[["lam"]]
currentAlpha <- parameterList[["alph"]]
currentDepth <- parameterList[["depth"]]
currentEta <- parameterList[["etaa"]]
xgb_params <- list("objective" = "multi:softprob",
"eval_metric" = "mlogloss",
"num_class" = 3,
"eta" = currentEta,
subsample = currentSubsampleRate,
colsample_bytree= currentColsampleRate,
min_child_weight=currentMCW,
lambda=currentLambda,
alpha=currentAlpha,
max_depth=currentDepth)
})
I did quite an extensive search but I always chose values in incremental steps, e.g., for eta I would try 0.1,0.15,0.2,… Using dials you might get to combinations that you didn’t think about but mostly it’ll optimise how to set the parameter combinations given the size parameter.
Next, we create a workflow from workflows that we will pass into the tuning object in the following step. We specify the formula for the model we want to fit based on the dependent variable outcome.
xgWorkflow <-
workflows::workflow() %>%
add_model(xgmodel) %>%
add_formula(outcome ~ .)
We can finally tune the model! We pass the workflow, cross-validation folds, grid of parameters to test and the metric we want to save from each model output. Note that metric_set comes from the yardstick package.
xgTuned <- tune_grid(
object = xgWorkflow,
resamples = cvFolds,
grid = xgGrid,
metrics = metric_set(mn_log_loss),
control = control_grid(verbose = TRUE))
Tuning the model on that grid took a while, around 90 minutes in a 8-core machine runing in parallel.
Since we are running parallelised code there is no progress output shown even though verbose is set to True.
Also, note that I set the trees parameter to 1000 in the model specification. This means that we are fitting 100 different XGBoost model and each one of those will build 1000 trees. XGBoost supports early stopping, i.e., you can specify a parameter that tells the model to stop if there has been no log-loss improvement in the last N trees.
Setting an early stopping criterion can save computation time. If there’s a parameter combination that is not performing well the model will stop well before reaching the 1000th tree.
Early stopping is currently not supported in the boost_tree function. However, according to this post it has been very recently implemented in the development version so you could give it a try if you were so inclined.
The xgTuned object contains the 100 combinations of parameters we tested and the corresponding mean log-loss from the cross-validation.
The show_best function outputs the best performing combinations.
xgTuned %>% tune::show_best(metric = "mn_log_loss") %>% kablify()
| mtry | min_n | tree_depth | learn_rate | sample_size | .metric | .estimator | mean | n | std_err |
|---|---|---|---|---|---|---|---|---|---|
| 19 | 8 | 6 | 0.0086232 | 0.8386232 | mn_log_loss | multiclass | 0.3126151 | 5 | 0.0056380 |
| 16 | 9 | 14 | 0.0153090 | 0.7279057 | mn_log_loss | multiclass | 0.3130304 | 5 | 0.0073298 |
| 42 | 19 | 12 | 0.0148805 | 0.7756686 | mn_log_loss | multiclass | 0.3147089 | 5 | 0.0067372 |
| 16 | 17 | 4 | 0.0147389 | 0.5218267 | mn_log_loss | multiclass | 0.3196296 | 5 | 0.0051067 |
| 39 | 26 | 9 | 0.0178508 | 0.4542553 | mn_log_loss | multiclass | 0.3210408 | 5 | 0.0061055 |
We can also get all the combinations with collect_metrics and we can plot them against mean log-loss.
xgTuned %>% collect_metrics() %>%
select(mean,mtry:sample_size) %>% data.table %>%
melt(id="mean") %>%
ggplot(aes(y=mean,x=value,colour=variable)) +
geom_point(show.legend = FALSE) +
facet_wrap(variable~. , scales="free") + theme_bw() +
labs(y="Mean log-loss", x = "Parameter")
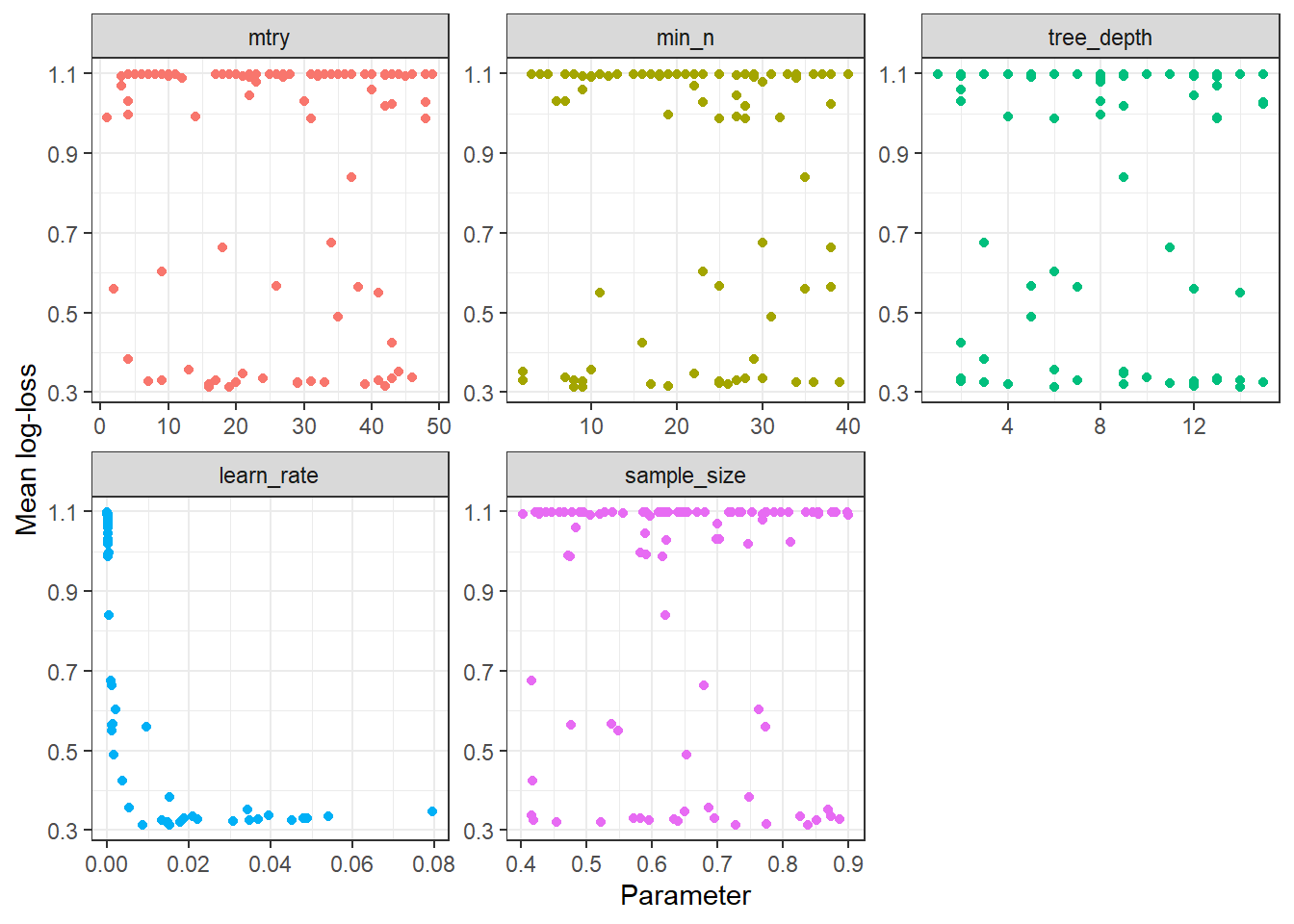
No clear patterns emerge from looking at the plots except that very small learn rate values lead to high log-loss. Having a grid that covers the parameter space as extensively as possible leads to many combinations that aren’t so great but the important point is that we get also get the ones that perform very well.
Fitting the best model
We can pick the best combination of parameters with select_best.
xgBestParams <- xgTuned %>% select_best("mn_log_loss")
The model is then finalised with those parameters with finalize_model and then the training data can be fit to it using fit
xgboost_model_final <- xgmodel %>% finalize_model(xgBestParams)
xgTrainFit<-xgboost_model_final %>% fit(outcome~., data=proc_mwTrainSet)
xgTrainFit
## parsnip model object
##
## Fit time: 1m 2.2s
## ##### xgb.Booster
## raw: 7.5 Mb
## call:
## xgboost::xgb.train(params = list(eta = 0.00862323672548215, max_depth = 6L,
## gamma = 0, colsample_bytree = 0.358490566037736, min_child_weight = 8L,
## subsample = 0.838623173511587), data = x, nrounds = 1000,
## verbose = 1, objective = "multi:softprob", num_class = 3L,
## lambda = 0, alpha = 1, nthread = 1)
## params (as set within xgb.train):
## eta = "0.00862323672548215", max_depth = "6", gamma = "0", colsample_bytree = "0.358490566037736", min_child_weight = "8", subsample = "0.838623173511587", objective = "multi:softprob", num_class = "3", lambda = "0", alpha = "1", nthread = "1", silent = "1"
## xgb.attributes:
## niter
## callbacks:
## cb.print.evaluation(period = print_every_n)
## # of features: 53
## niter: 1000
## nfeatures : 53
We can also get predictions on the training set; predict outputs the predicted classes while predict_classprob.model_fit outputs the class probabilities for each of the 3 classes.
xgTrainPreds<- xgTrainFit %>% predict(new_data=proc_mwTrainSet)
xgTrainPredProbs <- xgTrainFit %>% predict_classprob.model_fit(new_data=proc_mwTrainSet)
proc_mwTrainSet <- bind_cols(proc_mwTrainSet,xgTrainPreds,xgTrainPredProbs)
In the table below outcome is the dependent variable, .pred_class the predicted class and Type* are the class probabilities. As an example, in the first row Type2 has the highest probability so the prediction is assingnd to this class.
proc_mwTrainSet %>% select(Type1:outcome) %>% head %>% kablify()
| Type1 | Type2 | Type3 | .pred_class | outcome |
|---|---|---|---|---|
| 0.0591691 | 0.9169078 | 0.0239230 | Type2 | Type2 |
| 0.4554967 | 0.5316201 | 0.0128832 | Type2 | Type1 |
| 0.9568088 | 0.0382318 | 0.0049593 | Type1 | Type1 |
| 0.0451100 | 0.9463689 | 0.0085212 | Type2 | Type2 |
| 0.0335070 | 0.0201417 | 0.9463512 | Type3 | Type3 |
| 0.0105972 | 0.9814348 | 0.0079681 | Type2 | Type2 |
Model evaluation
We can evaluate the model using the yardstick package. The metrics function takes parameters truth and estimate and will output the accuracy and kappa metrics. If you pass the class probabilities it also calculates mean log-loss and roc_auc.
proc_mwTrainSet %>% yardstick::metrics(truth=outcome,estimate=.pred_class,Type1,Type2,Type3) %>% kablify()
| .metric | .estimator | .estimate |
|---|---|---|
| accuracy | multiclass | 0.9432000 |
| kap | multiclass | 0.9116029 |
| mn_log_loss | multiclass | 0.1906783 |
| roc_auc | hand_till | 0.9914153 |
When I first fit this model with XGBoost I got an accuracy of 0.96 and a validation log-loss of 0.306. So far with the current approach accuracy is at 0.943 and validation log-loss (from the xgTuned table in the previous section) at 0.313. I haven’t achieved results as good as I had before but I also have to note that getting to those values took me a lot of effort and going through the tuning process many times. Here, I did one pass and I’m already close. If I expand the tuning grid I could probably get better performance metrics.
We can also get the confusion matrix with conf_mat.
cm<-proc_mwTrainSet %>% yardstick::conf_mat(truth=outcome,estimate=.pred_class)
autoplot(cm, type = "heatmap")
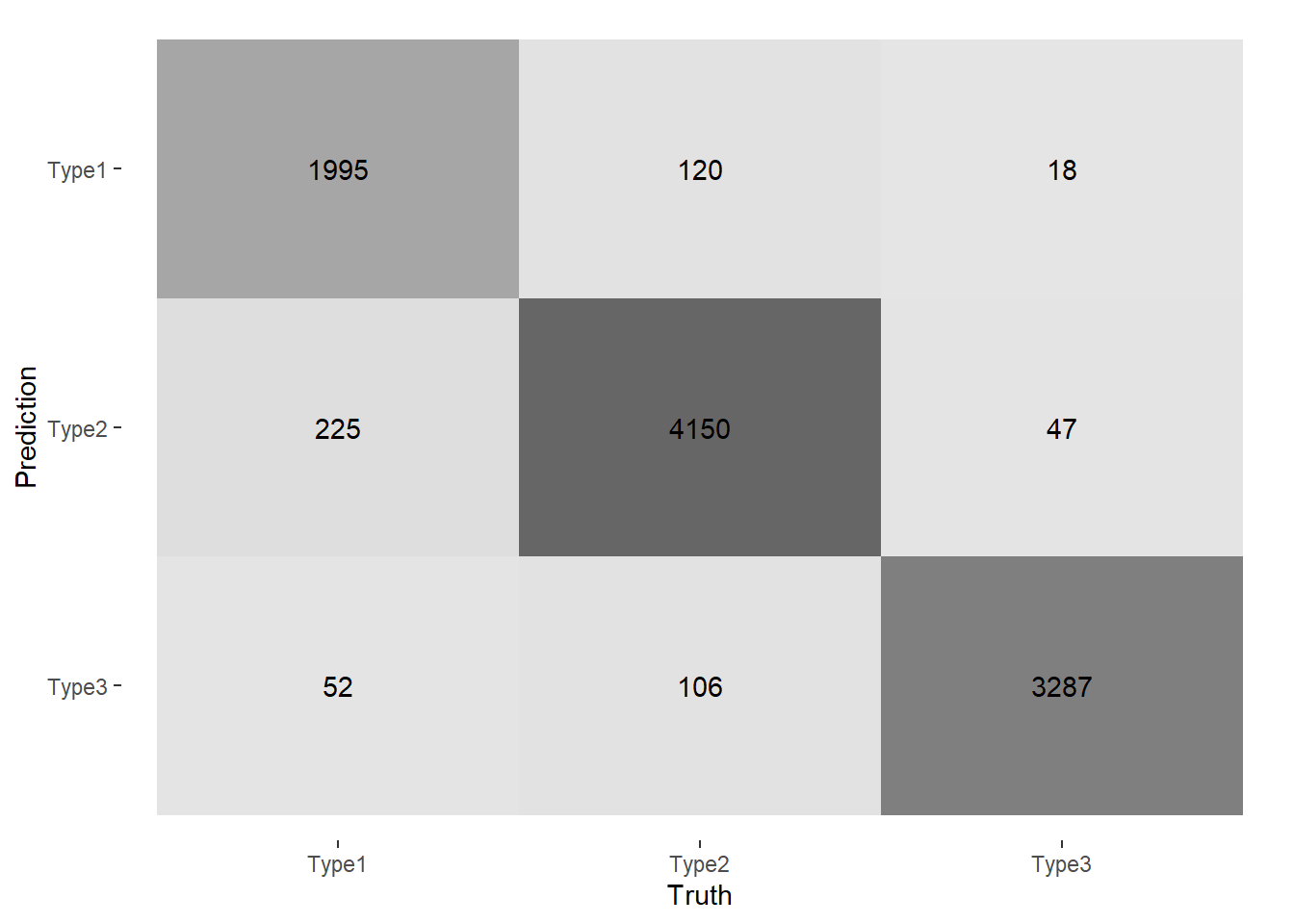
We can see that the Type3 class is better predicted than the other two.
In order to really finalise the model I would need to fit the test data and check the metrics in that set which has not been used in the modeling and hence provides an unbiased validation of out approach. I’m not going to focus on that here mainly because the test set did not come with labels so I won’t be able to calculate any performance metrics from it.
If this was a real life case, once you were happy with the results in the test set you could put the model into production and make predictions on new data.
Conclusions
This was a really quick tour around how tidymodels works. I think it has many advantages and it definitively makes the task of fitting reproducible ML models faster and more user-friendly so it is certainly something I will keep playing with.
I still think familiarity with the underlying models, in this case XGBoost, helps the user understand what this framework can and can’t do so I wouldn’t use it blindly without having some experience with the original model first.